Advances in Modeling the Generation of the Geomagnetic Field by the Use of Massively Parallel Computers and Profound Optimization

Thomas Clune
Silicon Graphics, Inc.
NASA Goddard Space Flight Center
Code 931
Greenbelt, MD 20771
clune@cray.com

Daniel S. Katz
Jet Propulsion Laboratory
Califonia Institute of Technology
4800 Oak Grove Drive, MS 168-522
Pasadena, CA 91109-8099
Daniel.S.Katz@jpl.nasa.gov

Gary A. Glatzmaier
IGPP, MS C305
Los Alamos National Laboratory
Los Alamo, NM 87545
gag@lanl.gov

Although people have been measuring and using the Earth's magnetic field for centuries, only during the 20th century has a ``back of the envelope'' theory arisen for the generation of the geomagnetic field by convection in the Earth's fluid outer core. Additionally, only within the last four years have dynamically self-consistent computer simulations of the geodynamo been achieved that finally validate much of the original convective dynamo theory and also provide many new insights and predictions. DYNAMO was the first simulation code to dynamically and self-consistantly model the evolution of the geomagnetic field, including its dominant dipolar structure, its westward drift of the non-dipolar part, the eastward super-rotation of the Earth's solid inner core, and magnetic dipole reversals, which take roughly five thousand years and occur roughly a couple times per million years. DYNAMO uses a spectral method (expansion in spherical harmonics and Chebyshev polynomials) that treats all linear terms implicitly and nonlinear terms explicitly [G.A. Glatzmaier and P.H. Roberts, ``An anelastic evolutionary geodynamo simulation driven by compositional and thermal convection,'' Physica D, 97, 81-94 (1996)] to model the magnetohydrodynamic equations that describe this problem. These equations are integrated over tens of millions of iterations, advancing the time dependent solution 20 days at a time.

To integrate the equations of motion over long times, DYNAMO uses the anelastic approximation which allows much larger time-increments, essentially by neglecting sound waves and thereby significantly altering the CFL criterion. The implicit treatment of the linear terms avoids the time step constraints related to diffusion. We have chosen a spectral method because it (1) greatly simplifies the magnetic boundary conditions, (2) has excellent accuracy characteristics and (3) allows a particularly simple representation of the Laplacian operator.

We have chosen to parallelize DYNAMO by distributing the data such that for each fundamental operation, the relevant data is local to the processor performing that operation. The alternative would have been to implement (at high cost in terms of software design and dubious performance gain) distributed matrix solvers as well as Legendre, Fourier and Chebyshev transforms. Currently, for any given operation, the data is distributed across a one-dimensional partition over the processors. We are in the process of adding the capability of two-dimensional partitioning so that a larger number of processors can be used for a given problem size and so that large grid sizes do not require each node to have a prohibitively large physical memory; in other words, so that a large problem can be run on currently available parallel computers.

The fundamental key for achieving high performance on virtually all massively parallel architectures is high cache reuse, and the CRAY T3E is no exception. With our parallelization strategy, it is quite straightforward to ensure that the data is arranged in a manner compatible with the aim of cache reuse. In fact, the Legendre transform can be reexpressed as a level 3 BLAS call to SGEMM (matrix-matrix multiplication) which achieves a substantial fraction of each processors peak speed. This is especially fortunate for larger grids where the $O(n^2)$ character of this operation tends to dominate the computational workload. We have used the vendor supplied Fourier transforms both directly for the azimuthal portion of the spherical transform as well as indirectly for the Chebyshev transform in the radial direction. Similarly, we have used the vendor supplied matrix operations SGEMM and SGETRS for the Legendre transforms and the matrix solves respectively.

A compromise to portability was made with the decision to implement most of the communications in SGI's proprietary, one-sided SHMEM communications library rather than MPI or PVM. The performance benefits for communication-intensive schemes such as spectral methods are significant, but we do hope to eventually implement software switches for using MPI on other platforms. Every effort was made to use long stride-1 packets which are optimal for message passing (including our current SHMEM implementation.) We also chose a communications ordering within the global transposes designed to substantially avoid network ``hotspots'' caused by contention.

A significant reduction (nearly a factor of 2) in the total workload is obtained by the recognition that the Legendre transforms can be coded to take advantage of the symmetry

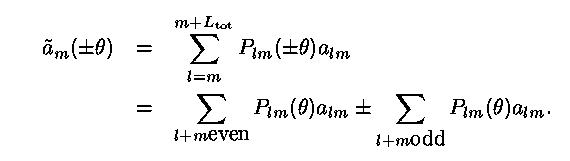
Thus, the transform for both the Northern and Southern hemispheres can be performed simultaneously for the same number of operations as required for a single hemisphere.

The T3E is especially favorable for distributed spectral codes, since the aggregate bandwidth through the torus is simply staggering. Because the total computational load grows as O(n⁴), while the communication only grows as O(n³), sufficiently large domains should typically scale well on most state-of-the-art MPP platforms.

Because the raw performance of the code increases with the resolution (due to the properties of the Legendre transform), it is difficult to simply characterize the performance of DYNAMO. Currently, we can sustain 105 Gflops on 427 nodes of a T3E-600 and 180 GF on 512 nodes of a T3E-1200. When the 2D partition scheme is completed, we should be able to scale up through 1024 nodes and sustain in excess of 200 GF on a T3E-600. Considering that previously, the sustained performance of DYNAMO was around 2 to 3 Gflops, the existence of this new version of DYNAMO represents a revolutionary breakthrough in the ability to model the geodynamo at ever increasing resolution, in order to eventually fully understand its mechanisms. More generally, this work is a powerful demonstration of the potential for using spectral methods on distributed memory machines.